Примеры сетевых топологий
Методики ограничений
Из-за особо сложной природы проблем надежности сетей с большим числом состояний, центром тяжести разработок в этой области является подготовка методик для ограничений различных систем метрик, представляющих интерес. Эти методики часто существенно отличаются от тех, что используются для проблем с двумя состояниями.
Исторически первой использовалась методика для аппроксимации надежности в стохастических сетях и среди них одна, которой уделялось наибольшее внимание, возникает из интуитивно привлекательной идеи, что ожидаемое значение E[Ф] длины кратчайшего пути/максимального потока/времени завершения может быть получено путем замены случайной длины/максимального потока/времени завершения для каждого ребра на детерминистский параметр, чье значение равно ожидаемой величине, и последующего решения детерминистского варианта проблемы. Это было фактически методикой решения, предложенной в оригинальном рассмотрении PERT в работе Малькольма и др. [D.G.Malcolm et al, “Application of a technique for research and development program evaluation”, Oper. Res. 7 (1959), 646-669]. Кажется фольклором то, что значение, полученное с помощью этой методики является верхней границей истинного значения ЕФ в проблеме PERT и нижней границей в проблемах наикратчайшего пути и максимального потока.
Наиболее успешные исследования концентрируются вокруг аппроксимации значения cdf F(a) =Pr[ФЈa] для Ф. Методика вначале была применена к проблеме PERT с непрерывными значениями параметров ребер, но может быть модифицирована для применения к проблемам кратчайшего пути, наибольшего потока и для случайных переменных ребра с дискретным распределением. В частности, предположим, что нужно вычислить число a, для которого FPERT(a)=b для некоторой специфицированной вероятности b. Заменяем каждую случайную переменную ребра Те на te, для которого Pr[TeЈ te]= b, и решаем для детерминистского значения наикратчайшего времени завершения. Полученная величина снова является верхней границей действительного времени завершения проекта, выдавая cdf значения b.
Улучшения выше описанной схемы для проблемы PERT заключается в вычислении для каждой вершины v в графе распределения для промежуточных случайных переменных
Фv= наидлиннейший маршрут до вершины v.
Во всех случаях вычисления производятся в топологическом порядке v1= s,v2,…,vn, т.е. все ребра, указывающие на vi исходят из вершин vj с j<i. Данная схема служит для вычисления нижней границы


суммирование производится по всем векторам b= ( bji: j<I) значений параметра, которые могут быть приняты для ребер, указывающих на вершину vi (члены, где (vj,vi) не существуют, игнорируются). Улучшения этой методики первоначально включали в себя оценки cdf значений Fi(a) для Фvi, в частности, вычисление верхней и нижней границы



Все они используют одну и ту же формулу с

Соответствующие ограничения для Е[Фvi] могут быть также упорядочены и их нижние ограничения лучше, чем полученные Фулкерсоном, нижние ограничения Фулкерсона и Кляйндорфера не могут быть единообразно сравнены. Ограничения Фулкерсона, Кляйндорфера и Шогана могут быть также модифицированы при использовании для проблемы кратчайшего пути (если исходный граф не содержит циклов) и для случая непрерывных параметров ребра. Ограничения Кляйндорфера априори вычисляемы за полиномиальное время.
Здесь мы предполагаем, что случайное значение пропускной способности Се является двоичным с ”рабочим” состоянием, представляющим нормальную пропускную способность се с вероятностью ре, и состоянием отказа, представляющим пропускную способность нуль с вероятностью 1-ре. Пусть Г1,…,Гr является набором всех цепочек (s,t) в G и пусть h1,…,hr равны потоку для каждого r цепочки (s,t). Этот значение потока верно, если для каждого ребра е в G, сумма потоков цепочки последовательных ребер, проходящих через е, меньше чем или равна пропускной способности е, а величина потока равна

Рассмотрим любую фиксированную цепочку потоков h1,…,hr, которая корректна для нормального набора пропускных способностей (се: eОE). В стохастической модели конкретная цепочка Гk может, следовательно, дать запрошенную долю потока hk, если и только если все ее ребра находятся в рабочем состоянии, в противном случае выдается нуль. Крайняя вероятность реализации этого равна, следовательно,

Метод группировки ребер и непересекающихся разрезов, обсужденные в разделах 4.2.1 и 4.2.2, предоставляют также эффективный способ расчета ограничений для проблем сетей с большим числом состояний. В частности, пусть Р1,…,Рq и Г1,…,Гr являются наборами разъединенных (s,t)-маршрутов и (s,t)-разрезов, соответственно. Эти два набора дают естественные верхние и нижние границы функций ФL и ФU для действительной функции Ф, зависящей от проблемы:
Кратчайший путь:

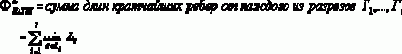
Максимальный поток:

Работоспособность сети PERT:
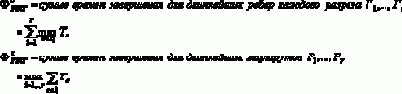
Эти функциональные ограничения в свою очередь дают естественные границы как для cdf, так и для действительной функции Ф, в частности,

и

Далее, каждая функция, описанная выше, состоит из одного min/max и одной свертки, поэтому cdf и ожидания для всех этих функций могут быть вычислены за полиномиальное время.
Две разные методики ограничений, представленные в разделе 4.2.4, были изучены в контексте проблем для систем со многими состояниями.
