Создание и редактирование векторных карт
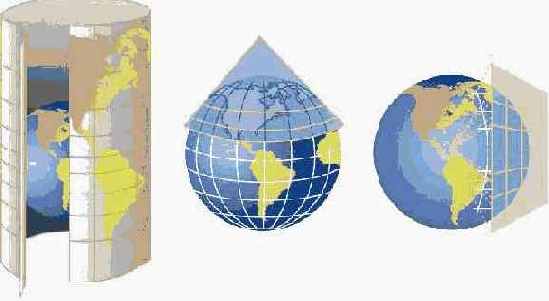
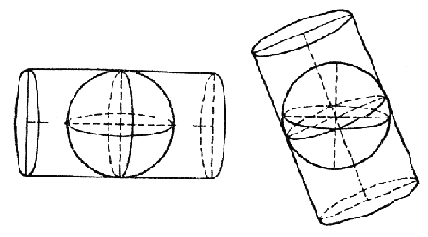
Цилиндрическая, конусная и плоскостная проекции.
Цилиндрическая, конусная и плоскостная проекции.
Бывают проекции равноугольные (конформные), равновеликие (эквивалентные) и произвольные. В равноугольных проекциях не искажаются углы: как пересекались дороги на местности под прямым углом, так будет прямой угол и на карте. В равновеликих не искажаются площади: как на местности было государство N кв. км, так будет и на карте, с учетом масштаба, разумеется. Разумеется, также, что форма государства на глобусе и на карте в такой проекции может сильно отличаться. И последний вид - произвольные проекции, в них искажаются и площади, и углы. Но зато на них смотреть приятнее, потому что картинки на таких картах больше похоже на те, что мы видим на глобусе. В общем, это компромиссный вариант между искажением углов и площадей.
Форма Земли Глобус как модель...
Форма Земли Глобус как модель Земли. Со сферы на плоскость. Проекции карт. О выборе проекций. Координатная сетка.
Эта лекция будет посвящена так называемой математической основе создания карт. Тем, кто в математике разбирается не очень, не стоит ждать здесь больших проблем. За весь материал Вам не встретится ни одной формулы. Ну может быть одна-две. Весь материал сделан в популярной форме и иллюстрирован рисунками. Основные знания по теме лекции Вам несомненно пригодятся в дальнейшем обучении и в реальной работе по созданию карт.
Форма Земли. Говоря о форме Земли...
Эллипс и его элементы.
Размеры любого эллипсоида вращения характеризуют большая а и малая b полуоси.
Отношение (a - b) / a называется сжатием эллипсоида. Эллипсоид вращения имеет математически правильную поверхность, образованную вращением эллипса вокруг его малой оси. Отступления по высоте точек поверхности геоида от поверхности наиболее близко подходящего к нему по своим размерам эллипсоида характеризуются в среднем величиной порядка 50 м и не превосходят 150 м. По сравнению с размерами Земли такие расхождения настолько незначительны, что на практике форму Земли принимают за эллипсоид. Эллипсоид, который характеризует фигуру и размеры Земли, называют земным эллипсоидом.
Установление размеров земного эллипсоида, наиболее близко подходящего по своей форме и размерам к фактической фигуре Земли, имеет большое научно-теоретическое и практическое значение. Это важно для создания точных топографических карт. Если размеры земного эллипсоида будут установлены неверно, то это приведет к неверным исчисленьям при проектировании на его поверхность, а следовательно, и при изображении на картах, всех длин линий и размеров площадей по сравнению с их действительными размерами на уровенной поверхности Земли. Размеры земного эллипсоида в разное время определялись многими учеными по материалам градусных измерений. Некоторые из них приведены в таблице:
| Автор определения | Страна, где опубликованы определения | Год определения | Большая полуось | Сжатие |
| Бессель | Германия | 1841 | 6 377 397 | 1 : 299,2 |
| Кларк | Англия | 1880 | 6 378 249 | 1 : 293,5 |
| Хейфорд | США | 1910 | 6 378 388 | 1 : 297,0 |
| Красовский | СССР | 1940 | 6 378 245 | 1 : 298,3 |
В США, Канаде, Мексике, Франции при создании карт пользуются размерами эллипсоида Кларка, в Финляндии и некоторых других странах - размерами эллипсоида Хейфорда, в Австрии — размерами эллипсоида Бесселя, в России и ряде других стран - размерами эллипсоида Красовского.
При решении некоторых практических задач, когда не требуется высокая точность, фигуру Земли принимают за шар, поверхность которого (около 510 млн. км2) равна поверхности эллипсоида принятых размеров. Радиус такого шара, вычисленный по элементам эллипсоида Красовского, равен 6371 116 м или округленно 6371 км.
Глобус, как модель Земли.
Глобус, как модель Земли.
Уменьшенной моделью Земли, наиболее полно отображающей ее поверхность, является глобус, что в переводе с латинского означает шар. С помощью глобуса можно представить себе вращение Земли вокруг оси, наклон земной оси к плоскости орбиты. А главное, на глобусе мы наблюдаем в уменьшенном виде всю поверхность нашей планеты.
Теперь ещё немного истории.
Первый упоминаемый в литературе земной глобус - глобус Кратеса из Пергамы - был сделан во II в. до н. э. Однако ни сам глобус, ни его изображение не найдены. В I в. н.э. среднеазиатский ученый Бируни, родившийся в городе Кяте - древней столице Хорезма, изготовил оригинальный глобус, наиболее точно для того времени передававший представление о земном шаре. О том, как ученый создавал свой глобус, он рассказывал сам: "Я начал с уточнения расстояний и названий мест и городов, основываясь на слышанном от тех, кто по ним странствовал, и собранном из уст тех, кто их видел. Предварительно я проверил надежность материала и принял меры предосторожности путём сопоставления сведений одних лиц со сведениями других". К сожалению и этот глобус до нас не дошел.
Первым из сохранившихся считается глобус, изготовленный в 1492 г. немецким географом М. Бехаймом. На нем еще не было Америки, и расстояние между западным побережьем Европы и восточным побережьем Азии было в два раза меньше, чем в действительности.
Уникальным памятником отечественной науки и техники XVIII в. является большой академический глобус, диаметр которого составляет 3 м 10 см. На наружной поверхности его нанесена карта Земли, а на внутренней- звездного неба. Глобус укреплен на железной оси, нижний конец которой упирается в пол, а верхний с помощью специальных растяжек крепится к стенам зала. Внутри глобуса на его оси смонтированы стол и скамья. Здесь могут разместиться одновременно 10-12 человек. С помощью особого механизма глобус вращается вокруг оси, а сидящие внутри зрители, оставаясь на неподвижной скамье, могут наблюдать движение небесных светил. Этот глобус хранится в музее М. В. Ломоносова в Санкт-Петербурге.
В настоящее время фигуру Земли представляют в виде эллипсоида, так как экваториальный радиус Земли больше полярного примерно на 21 км. Возникает вопрос, почему же глобусы изготовляют в виде шара, а не эллипсоида? Допустим, глобус имеет диаметр 50 см. В этом случае нетрудно посчитать, что разность экваториального и полярного радиусов глобуса составляет всего 0,1 см.
Понятно, что такое малое расхождение радиусов глобуса не может быть ощутимо. И действительно, с космических высот наша планета представляется правильным шаром с затуманенными из-за наличия атмосферы краями. Неровности земной поверхности также не отобразятся на глобусе. Даже такая величайшая вершина мира, как Джомолунгма, и та будет на глобусе незаметной песчинкой высотой несколько микрометров.
Обычно масштабы глобусов очень мелкие-1:30 - 1:80 млн., но в отдельных случаях, например у музейных глобусов, они составляют 1:10 млн. и крупнее. Такие глобусы иногда делают рельефными, но рельеф на них изображают в значительно укрупненном масштабе.
Параллели и меридианы, проведенные на глобусе, образуют своеобразную сетку, которая называется географической. Относительно этой сетки на поверхности глобуса изображены моря и океаны, материки и отдельные страны. Вследствие этого глобус обладает замечательными свойствами. Он не только наглядно представляет фигуру Земли, но и дает правильное представление о положении на земном шаре полюсов и экватора, а также основных частей земной поверхности: материков, океанов, морей, островов и других крупных объектов. Изображение Земли на глобусе имеет свойства равномасштабности, равновеликости и равноугольности. Это значит, что все линейные размеры даются на нем с одинаковым уменьшением, формы фигур подобны действительным очертаниям на земной поверхности, а площади всех объектов, показанных на глобусе, пропорциональны их действительным площадям на земном шаре.
Глобус как картографическая модель земного шара позволяет рассматривать Землю как бы со стороны, но не издалека и не окутанную в облачный покров, какой она видна из космоса, а расположенную рядом, доступную для непосредственного изучения, измерений и решения различных задач.
Картографические проекции
Так же картографические проекции различают:
- по характеру искажений на равноугольные, равновеликие и произвольные, включающие равнопромежуточные;
- по виду изображений параллелей и меридианов на цилиндрические, конические, азимутальные, поликонические, псевдоконические, псевдоцилиндрические, условные.
Применение тех или иных картографических проекций зависит от назначения карты, конфигурации и положения картографируемой территории.
Как уже быдл сказано, основными являются проекции на плоскость, конус и цилиндр. Плоские карты из конуса и цилиндра получаются разворачиванием их на плоскости. Это три способа, позволяющие представить поверхность земного шара на плоскости. Помещенный внутри глобуса источник света позволяет спроектировать очертания материков и градусную сетку на поверхность цилиндра, конуса или на плоскость. Большинство используемых картографических проекций получены с помощью одного из этих приемов. В каждом случае происходит некоторое искажение площадей, формы или расстояний.
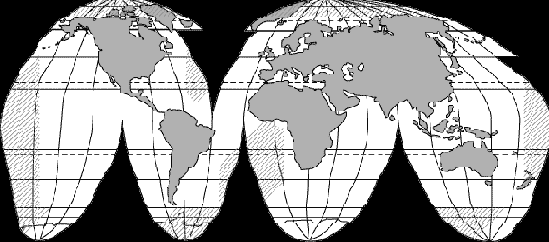
Комбинированная равновеликая проекция...
Комбинированная равновеликая проекция с разрывами, в которой низкие широты изображаются в синусоидальной проекции, а высокие – в проекции Мольвейде (псевдоцилиндрической). Часто карты в такой проекции даются в «сжатой форме», когда области, показанные на рисунке штриховкой, исключены.
Масштаб - вещь важная и, естественно, можно догадаться, что он в разных местах карты также будет разный. Вы, наверняка, вспомните карту Мира, где все меридианы выглядят параллельными. На такой карте отрезки параллелей между меридианами получаются везде одинаковые. А на глобусе, чем ближе к полюсу, тем отрезки параллелей между меридианами меньше. Вот и получается, что по параллелям масштаб в разных местах такой карты разный. Чем ближе к полюсам, тем масштаб крупнее. Разный масштаб в разных местах и на других картах, где географическая сетка меридианов и параллелей выглядит по иному, но этот вопрос мы с Вами опустим. Просто об этом надо помнить.
Проекции, при построении которых оси цилиндра или конуса совмещались с полярной осью земного шара, называются нормальными.
Еще проекции бывают косые, в которых наклон цилиндра или конуса относительно полярной оси составляет острый угол, и поперечные, когда этот угол составляет 90 градусов.
При описании проекций много внимания уделяется тому, как выглядят на них параллели и меридианы. Все знают, как они выглядят на глобусе, поэтому, изучая географическую сетку на карте в какой-либо проекции, можно понять, как и в каких местах эта карта искажена. По типу сетки можно выделить:
- Псевдоцилиндрические проекции, у которых параллели - прямые, параллельные друг другу, а меридианы - кривые, симметричные, относительно среднего прямолинейного меридиана,
- Псевдоконические, где параллели - дуги концентрических окружностей, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана,
- Поликонические, параллели которых - дуги эксцентрических окружностей с центрами на среднем прямолинейном меридиане, а меридианы - кривые, симметричные относительно среднего меридиана.
Помимо упомянутых проекций, существует ещё великое множество типов и разновидностей проекций. Каждая из них применяется для решения каких либо специальных задач. Некоторые из них созданы только для "красивости" отображения каких-то территорий Земли для гербов, знаков и т.п.
Я специально упускаю здесь подробности о составе, построении и множестве видов проекций. Если кого ни будь заинтересовала данная тема, то он всегда может получить исчерпывающую информацию из любой литературы, посвященной математическим основам картографии. Остановимся ещё немного на выборе проекций при решении различных картографических задач.
Координатная сетка.
Координатная сетка.
Важным элементом географической карты является сеть координатных линий — плоское изображение сети соответствующих линий на земном эллипсоиде. При изготовлении карты, сетка служит остовом для построения картографического изображения. При пользовании картой она позволяет определять координаты точек земного эллипсоида, наносить на карту точки по их координатам, измерять направление линий относительно стран света, вычислять масштабы и искажения в любом месте карты.
К самым распространенным сеткам, а на мелкомасштабных картах единственно употребляемым принадлежит картографическая — изображение сети меридианов и параллелей. Ценность картографической сетки обусловлена глубоким географическим смыслом меридианов и параллелей. Меридианы соответствуют направлению "Север — Юг", параллели — направлению "Запад — Восток". Этими направлениями, которые могут быть определены на местности, пользуются для ориентирования при работе с картой. Такое свойство картографической сетки существенно для топографических карт.
На мелкомасштабных картах картографическая сетка, представляет средство для широкого географического ориентирования, основу для разнообразных обобщений и выводов, вытекающих из широтной зональности в размещении многих природных явлений. Наконец, разность долгот пунктов выражает разность их времен.
При всех достоинствах географических сеток им свойствен один недостаток. Практические задачи - нанесение на карту точек по их географическим координатам или определение координат точек по карте, решаются с относительной простотой только на картах в цилиндрических проекциях, у которых меридианы и параллели образуют две системы взаимно перпендикулярных параллельных линий. В других проекциях с более сложными по виду картографическими сетками для решения указанных задач приходится прибегать к вспомогательным графическим построениям и вычислениям, осложняющим работу и не всегда выполнимым в полевых условиях. Между тем при использовании топографических карт для точного указания положения пунктов, передачи по карте расстояний, быстрого расчета направлений и расстояний и т. п. необходимы простые действия, которые могут быть обеспечены сеткой прямоугольных координат. Последняя показывается на современных топографических картах дополнительно к картографической сетке, а на некоторых картах (например, английских и финских) - взамен ее. С этой целью на земном эллипсоиде выбирают две системы линий, которые в проекции топографической карты изображаются сеткой квадратов. В проекции Гаусса-Крюгера осями такой сетки служат изображаемые прямолинейно осевой меридиан зоны и экватор.
В картографических сетках счет параллелей всегда ведут от экватора, счет меридианов — от начального меридиана, за который по международному соглашению 1884 г. принимают меридиан Гринвича, где находится старейшая астрономическая обсерватория Англии.
_______________
Контрольные вопросы.
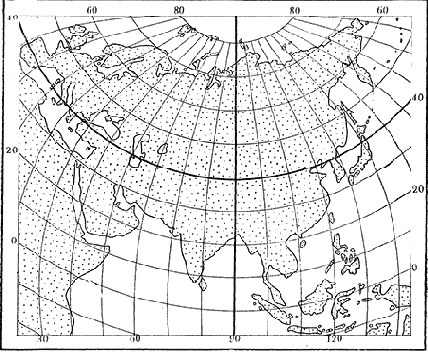
1. Какая проекция изображена на рисунке?
2. Какие проекции получатся из построений, показанных на рисунках?
3. Какие параметры надо учитывать при выборе проекции?
О выборе проекций.
О выборе проекций.
На выбор проекции для конкретной карты влияет ряд факторов, в первую очередь назначение карты и географические особенности территории.
Прежде всего, исходя из назначения карты, устанавливают предпочтительный характер искажений. Карты, используемые для измерения азимутов и углов, целесообразно строить в равноугольных проекциях. Например, для морских навигационных карт применяют равноугольную цилиндрическую проекцию Меркатора. Угол, измеренный на ней между направлением меридиана и направлением на конечный пункт, точно соответствовал курсу корабля. Хотя это и не будет кратчайшим путём.
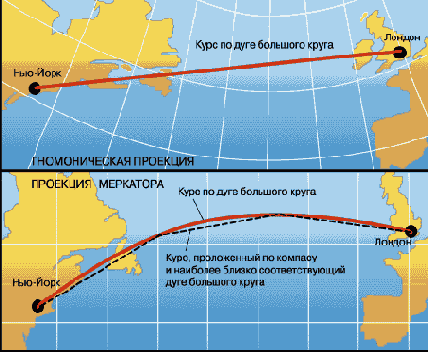
Общая длина пути на этих двух...
Общая длина пути на этих двух рисунках одинакова. На нижнем показана ортодромия.
На картах для целей телекоммуникации предпочитают косые стереографические проекции— радиоволны передающих станций распространяются по направлениям, которые в этой проекции изображаются прямыми линиями, и т. п. Опыт показывает, что равноугольные проекции удовлетворяют запросы многих потребителей. Однако при необходимости производить по картам измерения или сравнение площадей, что, например, существенно для некоторых экономических карт, обращаются к проекциям равновеликим. Когда чрезмерные искажения углов и площадей одинаково нежелательны, например, на картах полушарий, берут одну из произвольных проекций.
Учёт географических факторов, т. е. размеров, формы и положения картографируемой территории, позволяет найти в избранной группе проекций (равноугольных, равновеликих, произвольных) проекцию, обладающую наименьшими искажениями или их выгодным распределением, или другими ценными для карты свойствами.
Для карт мира преимущественно используют цилиндрические и псевдоцилиндрические проекции, имеющие сетки с прямолинейными и параллельными друг другу параллелями, что ценно при изучении явлений широтной зональности. В цилиндрических проекциях изображения повторяющихся территорий одинаковы. Чтобы уменьшить искажения в высоких широтах, можно строить проекцию на секущем цилиндре. Например, на многих картах Большого советского атласа мира была использована цилиндрическая проекция, сохраняющая главные масштабы по параллели 30°. Псевдоцилиндрические проекции по сравнению с цилиндрическими дают в высоких широтах меньшие искажения площадей, но увеличивают искажения углов, что сказывается особенно неблагоприятно на изображениях повторяющихся территорий, например Северной и Южной Америки.
Карты полушарий естественно строить в азимутальных проекциях. Ранее широко применялись равноугольная стереографическая проекция и равновеликая Ламберта. Первой из них на краях полушария свойственны большие искажения площадей. Поэтому в настоящее время для учебных карт предлагают произвольные азимутальные проекции, промежуточные по величине искажений.
Для карт отдельных материков (Европы, Азии, Северной Америки, Южной Америки, Австралии с Океанией) применяют преимущественно равновеликую косую азимутальную проекцию Ламберта с точкой нулевых искажений в центре изображаемого материка. Для Африки косая проекция заменяется экваториальной. В азимутальной проекции искажения нарастают по мере удаления от центра проекции и потому достигают наибольшей величины в углах прямоугольной рамки карты. Так, на карте Азии в пределах материка угловые искажения достигают 15°.
Карты России составляются главным образом в нормальных конических проекциях. Все нормальные конические проекции в их применения для карт России не позволяют показать точку полюса и вследствие значительной части кривизны параллелей как бы поднимают восточные и западные части СССР, что нарушает зрительное представление о широтных зонах. Эти недочеты, нежелательные для учебных карт, могут быть устранены при иной надлежаще подобранной проекции, хотя другие проекции обладают по сравнению с коническими проекциями большими искажениями.
В выборе проекций большую роль играет математический момент — величина искажений. Но этот признак не всегда решающий. Ярким примером этому служит использование для морских навигационных карт проекции Меркатора, которая при сохранении главного масштаба на экваторе преувеличивает площади на параллели 60° в 4 раза, а на параллели 80° более чем в 30 раз. Но в этой проекции курсы корабля изображаются прямыми линиями, а учет искажений длин, необходимый при определении пройденных расстояний, не вызывает затруднений.
Проекции карт.
Проекции карт.
Картографическая проекция - математически определенный способ отображения поверхности земного эллипсоида на плоскости. Картографическая проекция устанавливает аналитическую зависимость между географическими координатами точек земного эллипсоида и прямоугольными координатами тех же точек на плоскости.
В связи с тем что Земля, в общем, круглая, а карта абсолютно плоская, задача стоит так - круглую Землю отобразить на плоской карте, при этом не перерисовать, например, "Новую Землю" от руки, а спроецировать ее так, чтобы было установлено математическое соответствие между географическими координатами на Земле и плоскими координатами на бумаге. Для обеспечения этого математического соответствия и применяются проекции.
В картографической практике распространена классификация проекций по виду вспомогательной геометрической поверхности, которая может быть использована при ее построении. С этой точки зрения выделяют проекции: цилиндрические когда вспомогательной поверхностью служит боковая поверхность цилиндра, касательного к эллипсоиду или секущего эллипсоид; конические когда вспомогательной поверхностью является боковая поверхность касательного или секущего конуса; азимутальные
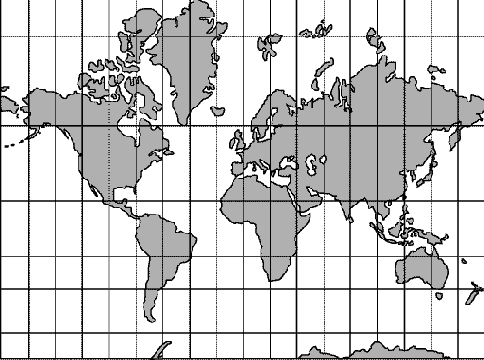
Проекция Меркатора. Хотя и весьма...
Проекция Меркатора. Хотя и весьма полезная для морских навигационных карт, приполярные области отображает с большими искажениями. Например, на этой карте сильно преувеличен размер Гренландии, которая в действительности меньше Аравийского п-ова.
В других случаях важно учитывать географические требования в отношении целостного изображения взаимосвязанных объектов, например, Атлантического и Северного Ледовитого океанов, наилучшего показа основных для темы карты пространств.
По мере уменьшения масштаба значение географических требований к выбору проекций возрастает. Напротив, для крупного и среднего масштабов на первый план выступает математический фактор. Карты этих масштабов часто используются в инженерных и оборонных целях, вследствие чего измерения по ним должны отличаться простотой и давать результаты большой точности. Это возможно при практически неощутимых искажениях. Однако при изображении обширных территорий любая проекция дает крупные искажения. Выход был найден в первой половине XIX в., когда стали применять так называемые многогранные проекции (точнее, многогранные построения), когда проекция вычисляется особо для каждого отдельного листа многолистной карты.
Как Вам уже известно, искажения возрастают по мере удаления от точек или линий, сохраняющих главный масштаб. В равноугольных проекциях искажения длин увеличиваются пропорционально квадрату этого удаления. Из этого можно сделать вывод, что при картографировании ограниченного пространства практически можно не учитывать искажений длин и считать в этом смысле различные равноугольные проекции равноценными. Это значит, что при создании карт на большую территорию можно ограничить искажения пренебрегаемыми величинами, если изображать ее по частям. Для этого есть разные пути.
Первоначально прибегали к замене земного эллипсоида многогранником, вписанным в эллипсоид (или описанным около него), и самостоятельному изображению отдельных граней.
Позднее для топографических карт многих стран стали использовать равноугольную поперечную цилиндрическую проекцию Гаусса-Крюгера, нередко называемую поперечной цилиндрической Меркатора. Для ее применения поверхность эллипсоида разделяется на сфероидические двуугольники (геодезические зоны), каждый из которых изображается на плоскости самостоятельно.
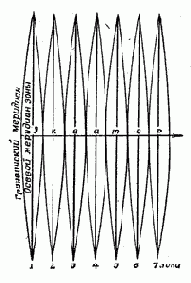
Таким образом «многогранная проекция» заменена «многополосной». Она создает разрывы по краям зон, но позволяет соединять в одно целое листы внутри всей зоны и считать в пределах зоны масштаб практически постоянным. Именно с такой проекцией нам. в большинстве случаев, и придётся иметь дело.
Равнопромежуточная цилиндрическая проекция.
Равнопромежуточная цилиндрическая проекция.
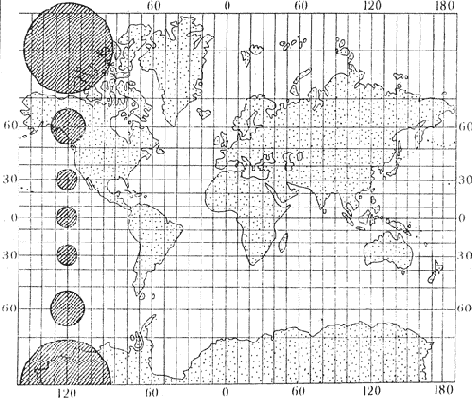
Равноугольная цилиндрическая проекция.
Равноугольная цилиндрическая проекция.
Применяя различные картографические проекции, можно создавать карты, свободные или почти свободные от одних искажений, но сохраняющие искажения другого рода. Знакомясь с различными видами карт, можно только поражаться широте возможностей и гибкости средств, которыми обладает картография. Картографы могут предложить специалистам множество проекций, причем каждая будет удовлетворять ранее заданным условиям, за исключением одного: карты, совершенно свободной от искажений земной поверхности, не существует. Хотите избавиться от одних искажений - миритесь с другими!
Самые большие искажения свойственны картам мира, так как на них изображают поверхность всего земного шара. На картах отдельных стран искажения будут меньше. Это легко понять: ведь маленькую выпуклость сферы легче перенести на плоскость! Поэтому на карте, изображающей небольшой материк, небольшую страну, разномасштабность в различных ее местах невелика, и при измерениях можно пользоваться одним, средним масштабом.
На первый взгляд, построение картографических проекций может показаться простым делом. На самом же деле любая проекция строится по строгому математическому закону. Изучением законов построения картографических проекций занимается специальная наука - математическая картография.
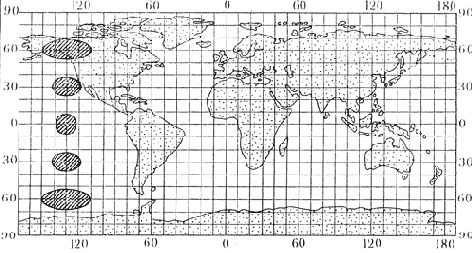
Равновеликая цилиндрическая проекция.
Равновеликая цилиндрическая проекция.
Со сферы на плоскость.
Со сферы на плоскость.
Глобус, безусловно, даёт самое верное представление о взаимном расположении материков и океанов, рек, городов, гор. Но с этой моделью нашей планеты не очень удобно работать. Глобусы при всех своих достоинствах очень мелкомасштабны и громоздки. Так, если бы глобус был изготовлен в масштабе 1:1 000 000, то он имел бы диаметр 12,7 м. Кроме того, на нем трудно производить линейные измерения, определять плановые координаты точек, наносить на него изображения географических объектов. Да и пользоваться глобусом не всегда удобно - ведь его нельзя напечатать в книге или на отдельном листе. Поэтому глобусы имеют меньшее распространение и применение, чем карты, которые более удобны для использования и хранения.
Как же перейти от глобуса к карте, как перенести сферическую поверхность Земли на плоскость? Если бы Земля имела форму цилиндра или конуса, то сделать развертку ее поверхности не составило бы больших трудностей. Но попробуйте сделать плоской корку от апельсина и вы поймете, в чём заключается основная проблема картографии: поверхность шара или эллипсоида нельзя перенести на плоскость без разрывов или складок.
Попытаемся сделать так. Перенесем с поверхности глобуса узкие полоски, ограниченные меридианами через 10 или 15° по долготе. В пределах каждой полоски видимых искажений нет, но зато между полосками получились разрывы, которые увеличиваются по мере удаления к полюсам. Заполним эти разрывы слегка растянув картографические рисунки, изображающие земную поверхность. Из-за этого правда, расстояния между городами, размеры морей, островов станут большими, чем на глобусе. Гренландия, например, будет выглядеть больше, чем Австралия, хотя на самом деле ее площадь в 3 раза меньше. На глобусе, конечно, таких сюрпризов нет. Но уж тут ничего не поделаешь - другого выхода нет. Приходится с подобными искажениями мириться Важно только знать, в каком участке карты и на сколь ко растянуты изображения.
Заметьте, что на каждой полоске, вырезанной из глобуса, крайние меридианы, а также параллели были дугами окружностей, а на карте они после растяжения стали прямыми линиями. Таким образом, переход от поверхности глобуса к плоскости получился в результате преобразования градусной сетки глобуса. В этом и состоит сущность так называемых картографических проекций.
В зависимости от вида проекции меридианы и параллели, образующие градусную или картографическую сетку, могут изображаться прямыми, или кривыми линиями. Сетка параллелей и меридианов служит основой любой карты. Ее заполняют географическими объектами, положение которых определяется из топографических съемок. Образно говоря, сетка служит канвой, на которой вышиваются географические узоры.
При создании карт применяют самые разнообразные проекции. Точки земной поверхности проектируют на плоскости, конусы, цилиндры, многоугольники или сразу же на поверхности нескольких совмещенных фигур. При этом Земля принимает самый разнообразный вид.
Над разработкой картографических проекций трудились крупнейшие ученые разных эпох. Достаточно назвать Аристотеля и Птолемея, Леонардо да Винчи и Декарта, М. В. Ломоносова и К. Гаусса. Замечательный русский ученый, создатель периодической системы химических элементов Д. И. Менделеев также внес определенный вклад в картографию: он предложил оригинальную проекцию для карты России, и такая карта была издана в 1906 г.
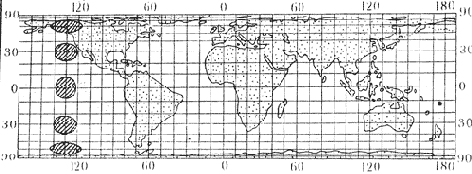
Несмотря на то, что существуют тысячи способов изображения Земли на плоскости, ни один из них не дает точного ее воспроизведения. Всегда чем-то приходится жертвовать. На одних картах правильно изображают очертания материков и океанов, но при этом искажают их размеры. На других - сохраняют площади, зато искажают формы континентов. Ниже, с помощью эллипсов, показаны искажения, которые имеют место в некоторых проекциях.